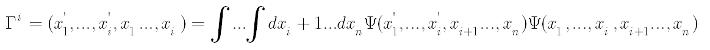De elektron golffunctie is de ultieme informatiebron die alle (elektronische) eigenschappen van een molecule bepaalt.Voor praktische berekeningen is dit echter een te gecompliceerd object. De meest essentiële informatie is vervat in de zogenaamde dichtheidsmatrices

De 2de orde dichtheidsmatrix bevat bijvoorbeeld alle informatie omtrent de elektronische energie van het systeem. De 1ste orde dichtheidsmatrix levert dan weer de populaire natuurlijke orbitalen.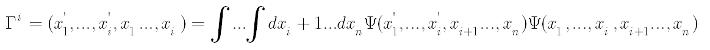

Concepten zoals atomen en functionele groepen zijn in deze kwantumfysische benadering van moleculen volledig afwezig. Nochtans zijn dergelijke informatieshortcuts erg succesvol gebleken in de ontwikkeling van de moderne scheikunde. Chemische reactiviteit wordt begrepen in termen van atomaire ladingen, bindingsenergieen, nucleofiele en elektrofiele functionele groepen, elektronduwende en elektronzuigende groepen, basische en zure groepen,... Een kwantumfysische definitie van atomen en functionele groepen zou toelaten deze typische chemische parameters te eenvoudig en eenduidig te kwantificeren en catalogeren.

Tot dusver werden kwantumfysische atomen steeds geconstrueerd op het niveau van de elektronische densiteit (=de diagonaal van de 1ste orde densiteitsmatrix). Afhankelijk van de gebruikte definitie van atomen binnen moleculen (AIM ='atoms in molecules') werden uiteenlopende resultaten bekomen voor de berekende AIM eigenschappen, zoals de effectieve atomaire ladingen (Mulliken, Bader, Hirshfeld,...).

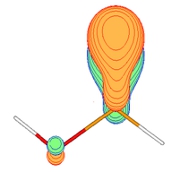
Een hot topic in de kwantumchemie is dan ook het uitbreiden van de kwantumfysische AIM's tot op het niveau van de 1ste orde dichtheidsmatrix [1]. Dit levert ons essentiele informatie hoe een molecuulorbitaal tot stand komt vanuit atomische orbitalen. Verdere uitbreiding tot op het niveau van de 2de orde dichtheidsmatrix zou toelaten een gedetailleerd inzicht te verkrijgen in de energetische aspecten van bindingsvorming (energiedeconvolutie). Binnen dit onderwerp kan je vele kanten uit: een bestaande methode uitbreiden tot het niveau van de 1ste of 2de orde dichtheidsmatrix of meewerken aan het ontwikkelen van een nieuw algoritme voor de definitie van atomen en bindingen in moleculen. Het thesiswerk omvat dus het bedenken en implementeren van diverse partitioneringsalgoritmes en het uitvoeren van grootschalige numerieke testen.

[1] D. Vanfleteren, D. Van Neck, P. Bultinck, P. W. Ayers, M. Waroquier, Partitioning of the molecular density matrix over atoms and bonds, J. Chem. Phys., 132, 164111 (2010).
[2] D. Vanfleteren, D. Van Neck, P. Bultinck, P. W. Ayers, M. Waroquier, Hilbert-space partitioning of the molecular one-electron density matrix with orthogonal projectors, J. Chem. Phys.,133(23), 231103 (2010)